专插本：我院数学与应用数学（师范）专业2020年招收120名本科插班生

为了进一步贯彻落实全国教育大会精神，选拔优秀专科生升入本科高校继续深造，为地方培养优秀的数学师范人才，我院数学与应用数学（师范）专业计划于2020年招收120名本科插班生。欢迎2020届数学教育专科毕业生及数学类专业专科毕业生报考。具体招生计划如下：

肇庆学院2020年本科插班生招生计划
序号	学院	专业名称	招生计划	是否师范生
1	经济与管理学院	国际经济与贸易	120
		会计学	120
		市场营销	60
		小   计	300
2	教育科学学院	学前教育（师范）	50	是
		小学教育（师范）	100	是
		小   计	150
3	文学院	汉语言文学（师范）	200	是
		小   计	200
4	外国语学院	英语（师范）	225	是
		小   计	225
5	数学与统计学院	数学与应用数学（师范）	120	是
		小   计	120
6	生命科学学院	生物技术（师范）	40	是
		生物科学（师范）	100	是
		小   计	140
7	计算机科学与软件学院、大数据学院	计算机科学与技术（师范）	20	是
		小   计	20
8	环境与化学工程学院	环境工程	50
		小   计	50
9	食品与制药工程学院	食品科学与工程	60
		小   计	60
10	旅游与历史文化学院	酒店管理	50
		旅游管理	100
		小   计	150
总计			1415

 

咨询电话：0758-2716327；0758-2751331

 

 

附1：专业课程考试考试科目和参考书：

 

2020年本科插班生招生数学与应用数学(师范)专业考试科目和参考书

 

 

 

 

 

 

 

 

 

附2：专业课程考试大纲：

 

2020年本科插班生考试大纲

（校考专业课：数学分析）

Ⅰ考试性质

普通高等学校本科插班生（又称专插本）招生考试是由专科毕业生参加的选拔性考试。高等学校根据考生的成绩，按照已确定的招生计划，德、智、体全面衡量，择优录取。因此，本科插班生考试应有较高信度、效度、必要的区分度和适当的难度。

 

Ⅱ考试内容及要求

第一章  实数集与函数

一、实数（识记）

实数及其性质；绝对值与不等式。

二、数集·确界原理（识记）

区间与邻域；有界集，确界原理。

三、函数概念（理解、掌握）

函数的定义，函数的表示法，函数的四则运算，复合函数，反函数，基本初等函数和初等函数。

四、具有某些特性的函数（理解、掌握）

有界函数，单调函数，奇函数和偶函数，周期函数。

第二章  数列极限

一、数列极限的概念（理解、掌握）

数列极限的定义；无穷小数列的定义。

二、收敛数列的性质（识记、理解）

唯一性、有界性、保号性、保不等式性、迫敛性、四则运算法则。

三、数列极限存在的条件（理解）

单调有界定理；Cauchy收敛准则。

第三章  函数极限

一、函数极限的概念（理解、掌握）

x趋于时函数的极限（定义）；x趋于时函数的极限()。

二、函数极限的性质（理解、掌握）

唯一性、局部有界性、局部保号性、保不等式性、迫敛性、四则运算法则。

三、函数极限存在的条件（理解）

归结原则；单调有界定理；Cauchy准则。

四、两个重要极限（理解、应用）

 

 

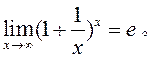
五、无穷小量与无穷大量（识记）

无穷小量，无穷小量阶的比较；无穷大量。

第四章  函数的连续性

一、连续性概念（理解、掌握）

函数在一点的连续性；间断点及其分类；区间上的连续函数。

二、连续函数的性质（理解）

连续函数的局部性质（局部有界性、局部保号性、四则运算性、复合函数的连续性）；闭区间上连续函数的性质（有界性、最值性、介值性、零点定理）；反函数的连续性；一致连续性。

三、初等函数的连续性（理解、掌握）

基本初等函数的连续性；初等函数的连续性。

第五章  导数和微分

一、导数的概念（掌握）

导数定义，导函数，单侧导数，导数的几何意义。

二、求导法则（掌握）

基本求导公式，四则运算求导法则，复合函数与反函数的求导法则，隐函数与参数方程的求导法则，高阶导数。

三、微分（识记、理解）

微分的概念，微分的运算法则，微分在近似计算中的应用。

第六章  微分中值定理及其应用

一、微分中值定理（理解）

罗尔中值定理，拉格朗日中值定理，柯西中值定理。

二、泰勒公式（识记）

泰勒定理，某些初等函数的泰勒展式。

三、导数的若干应用（掌握、应用）

不定式极限；函数的单调性与极值；函数的最大值与最小值；函数的凹凸性及拐点、渐近线；实际问题中的最值。

第七章  实数的完备性

一、实数集完备性基本定理（识记）

区间套定理、聚点定理、有限覆盖定理、确界原理、单调有界定理、柯西收敛准则。

二、利用实数完备性定理证明闭区间上连续函数的基本性质（识记）

第八章  不定积分

一、不定积分的概念与基本积分公式（掌握）

原函数与不定积分的概念，基本积分表，线性运算法则。

二、基本积分方法（掌握）

换元积分法，分部积分法。

三、有理函数和可化为有理函数的不定积分（理解）

有理函数的不定积分，三角函数有理式的不定积分，简单无理函数的不定积分。

第九章  定积分

一、定积分概念（理解、掌握）

定积分概念背景，定积分定义。

二、可积条件（识记）

可积的必要条件，可积的充分条件，可积函数类。

三、定积分的性质（理解、掌握）

线性性质，积分区间的可加性，单调性，绝对可积性，积分中值定理。

四、微积分学基本定理（理解、掌握）

五、定积分的计算（掌握）

牛顿--莱布尼兹公式，换元积分法，分部积分法。

第十章  定积分的应用

一、定积分的几何应用（理解、应用）

平面图形的面积、旋转体的体积、平面曲线的弧长、旋转曲面的面积。

二、定积分的物理应用（选学，不做考核要求）

第十一章  反常积分

一、反常积分概念（理解）

无穷积分；瑕积分

二、反常积分的性质与收敛判别（识记、理解）

无穷积分的性质与收敛判别；瑕积分的性质与收敛判别。

第十二章  数项级数

一、级数的收敛性（理解、掌握）

无穷级数的收敛、发散、级数的和等概念；收敛级数的基本性质；柯西准则。

二、正项级数（理解、掌握）

收敛原理，比较原则，达朗贝尔判别法，柯西判别法，积分判别法。

三、一般项级数（识记、理解）

交错级数与莱布尼兹判别法；绝对收敛与条件收敛；阿贝耳判别法与狄利克雷判别法。

第十三章  函数列与函数项级数

一、收敛与一致收敛性（理解、掌握）

函数列的收敛、收敛域、极限函数等概念；函数项级数的和函数；函数列与函数项级数的一致收敛性。

二、函数列与函数项级数一致收敛性判别法（理解）

一致收敛柯西准则，维尔斯特拉斯优级数判别法，阿贝耳判别法与狄利克雷判别法。

三、函数列的极限函数与函数项级数和函数的分析性质（理解）

连续性，可积性（逐项积分），可微性（逐项微分）。

第十四章  幂级数

一、幂级数（理解、掌握）

阿贝尔第一定理；收敛半径与收敛区间；一致收敛性；和函数的连续性、可积性、可微性。

二、函数的幂级数展开（识记、理解）

泰勒级数；函数展开为幂级数的条件；初等函数的幂级数展开式。

 

第十五章  傅里叶级数

一、傅里叶级数（识记、理解）

三角级数；正交函数系；以为周期的函数的傅里叶级数；收敛定理。

二、以为周期的函数的展开式（识记）

以为周期的函数的傅里叶级数；奇函数与偶函数的傅里叶级数。

三、收敛定理的证明（识记）

第十六章  多元函数的极限与连续

一、平面点集与多元函数（识记、理解）

平面点集的基本概念：邻域，内点、界点，聚点，孤立点，开集，闭集，区域，开区域，闭区域；上的完备性定理；多元函数。

二、二元函数的极限（识记、理解）

二元函数的极限；累次极限。

三、二元函数的连续性（识记、理解）

二元函数的连续性概念；有界闭域上连续函数的性质（有界性、介值性、最值性、一致连续性）。

第十七章  多元函数微分学

一、可微性（理解、掌握）

可微性与全微分，偏导数，可微性条件，可微性几何意义与应用。

二、复合函数微分法（理解、掌握）

复合函数的求导法则，复合函数的全微分；

三、方向导数与梯度（理解）

四、泰勒公式与极值问题（理解）

高阶偏导数，中值定理与泰勒公式，极值问题。

第十八章  隐函数定理及其应用

一、隐函数（理解、掌握）

隐函数概念，隐函数存在定理，隐函数求导方法。

二、隐函数组（识记）

隐函数组概念，隐函数组定理，反函数组与坐标变换。

三、几何应用（识记）

平面曲线的切线与法线，空间曲线的切线与法平面，曲面的切平面与法线。

四、条件极值-拉格朗日乘数法（理解）

第十九章  含参量积分（选学）

一、含参量正常积分（识记）

参量正常积分的定义，参变量正常积分的性质（连续性、可导性、可积性）。

二、含参量非正常积分（识记）

含参量非正常积分的定义与收敛准则、性质；一致收敛及其判别法；欧拉积分（函数，B函数）。

第二十章  曲线积分

一、曲线积分（理解、掌握）

第一型曲线积分的概念与计算，第二型曲线积分的概念与计算。

二、两类曲线积分间的联系（识记）

第二十一章  重积分

一、二重积分的概念（理解）

二重积分的定义及其存在性，二重积分的性质。

二、二重积分的计算（掌握）

二重积分化为累次积分，二重积分换元法，极坐标换元。

三、格林公式（理解、掌握）

格林公式，平面上曲线积分与路径无关性。

四、三重积分（理解、掌握）

三重积分的定义与性质，三重积分化为累次积分，三重积分换元法。

五、重积分的简单应用（识记）

立体体积，曲面面积，质量和重心的计算，转动惯量，引力。

第二十二章  曲面积分

一、曲面积分（理解、掌握）

第一型曲面积分的概念与计算，曲面的侧，第二型曲面积分的概念与计算，

两类曲面积分的联系。

二、高斯公式与斯托克斯公式（理解）

 

 

Ⅲ.考试形式及试卷结构

一、考试形式：

闭卷、笔试。考试时间120分钟，满分100分。考生使用答题卡答题。

二、知识内容比例：

1.一元函数的极限（含数列极限）与连续性   约占20%

2.一元函数微积分学（含数列极限）         约占40%

3.数项级数、函数项级数                   约占20%

4.多元函数微积分学                       约占20%

其中,识记部分约占25%，理解部分约占40%，应用部分约占35%。

三、试题难易比例：

    容易题………………………约占30%

    中等难度题…………………约占50%

    难题…………………………约占20%

四、试题题型及赋分：

1．填空题………………………约占18%

2. 单项选择题…………………约占18%

    3．判断题………………………约占10%

    4．计算题………………………约占36%

5．应用题………………………约占8%

6．证明题………………………约占10%

 

 

 

 

 

2020年本科插班生考试大纲

（校考专业课：高等代数）

Ⅰ 考试性质

普通高等学校本科插班生（又称专插本）招生考试是由专科毕业生参加的选拔性考试。高等学校根据考生的成绩，按照已确定的招生计划，德、智、体全面衡量，择优录取。因此，本科插班生考试应有较高信度、效度、必要的区分度和适当的难度。

 

Ⅱ 考试内容及要求

一、考试基本要求

要求考生理解和掌握《高等代数》的基本概念、定理、性质和方法，能运用本门课程的基础知识和基本方法进行判断、分析、计算和证明；应具有较好的抽象思维能力、逻辑推理能力、运算能力；具备一定的分析、解决问题的能力．

二、考核知识点和考核要求

本大纲的考核要求分为“了解”、“理解”、“掌握”与“熟练掌握”四个层次：

1、了解：对知识的涵义有感性的、初步的认识，能在相关问题中正确地识别和表述．

2、理解：对概念和定理、性质等规律达到了理性认识，能知其然，也能知其所以然，能理解有关概念和定理、性质与其他概念、规律的联系，知其用途．

3、掌握：在理解的基础上形成技能、方法，并用来解决一些问题．

4、熟练掌握：达到灵活应用的程度．

第一章  多项式

（一）考核知识点

1.数域（了解）；

2.一元多项式的定义及运算（了解）；

3.多项式的整除性，带余除法（熟练掌握）；

4.最大公因式.辗转相除法.互素（熟练掌握）

5.不可约多项式，因式分解及唯一性（掌握）；

6.重因式（掌握）；

7.多项式函数及根（掌握）；

8.复数域.实数域上的多项式.代数基本定理（理解）；

9.有理数域上的多项式.整系数多项式.Eisenstein判别法（理解）；

（二）考核要求

1.了解数域

2.了解一元多项式的定义及运算；

3.熟练掌握多项式的整除性，带余除法；

4.熟练掌握最大公因式.辗转相除法.互素；

5.掌握不可约多项式，了解因式分解及唯一性；

6.掌握重因式；

7.掌握多项式函数及根；

8.理解复数域.实数域上的多项式.代数基本定理；

9.理解有理数域上的多项式.整系数多项式.Eisenstein判别法；

第二章  行列式

（一）考核知识点

1.排列的逆序数与奇偶性（了解）；

2.行列式的定义（理解）；

3.行列式的计算与Vandermonde行列式（熟练掌握）；

4.行列式的性质和行列式的展开（熟练掌握）；

5.Cramer法则（掌握）；

（二）考核要求

1.了解排列的逆序数与奇偶性；

2.理解行列式的定义；

3.熟练掌握行列式的计算与Vandermonde行列式；

4.熟练掌握行列式的性质和行列式的展开；

5.掌握Cramer法则；

第三章  线性方程组

（一）考核知识点

1.消元法，阶梯矩阵，矩阵消元法（掌握）；

2.n维向量空间（理解）；

3.线性相关，线性无关，向量组的极大线性无关组与秩（掌握）；

4.矩阵的秩，子式（理解）；

5.线性方程有解判别定理（熟练掌握）；

6.线性方程组解的结构，导出组基础解系（理解）；

（二）考核要求

1.掌握消元法，阶梯矩阵，矩阵消元法；

2.理解n维向量空间；

3.掌握线性相关，线性无关与向量组的秩的定理与推论，熟练掌握线性相关性的判定与向量组的极大线性无关组与秩的求法；

4.理解矩阵的秩，子式的概念，熟练掌握求矩阵的秩；

5.熟练掌握线性方程有解判别定理；

6.理解线性方程组解的结构，导出组基础解系，熟练掌握求解线性方程组；

第四章  矩阵

（一）考核知识点

1.矩阵的概念和运算（熟练掌握）；

2.矩阵乘积的行列式，乘积的秩（熟练掌握）；

3.矩阵的初等变换，初等矩阵.初等变换和初等矩阵的关系（熟练掌握）；

4.可逆矩阵，求逆矩阵的两种方法（用伴随矩阵的方法以及用初等变换的方法）（熟练掌握）；

5.分块矩阵及其运算规则（了解）；

（二）考核要求

1.熟练掌握矩阵的概念和运算；

2.熟练掌握矩阵乘积的行列式的概念与求法，理解矩阵乘积的秩；

3.熟练掌握矩阵的初等变换，初等矩阵.理解初等变换和初等矩阵的关系；

4.熟练掌握可逆矩阵以及求逆矩阵的两种方法（用伴随矩阵的方法以及用初等变换的方法）；

5.了解分块矩阵及其运算规则；

第五章 二次型

（一）考核知识点

1.二次型的矩阵表示，矩阵的合同（熟练掌握）；

2.二次型的标准形（掌握）；

3.复数域.实数域上二次型的规范形（理解）；

4.正定二次型.正定矩阵及其判定方法（掌握）；

（二）考核要求

1.熟练掌握二次型的矩阵表示，理解矩阵的合同；

2.掌握二次型的标准形概念及求法；

3.理解复数域.实数域上二次型的规范形；

4.掌握正定二次型.正定矩阵及其判定方法；

第六章  线性空间

（一）考核知识点

1.线性空间的定义和性质（了解）；

2.线性空间的基与维数，基的过渡矩阵及其性质（理解并熟练掌握）；

3.子空间的定义和判定条件，子空间的运算，维数公式（理解）；

4.线性空间的和与直和（掌握）；

5.线性空间的同构（理解）；

（二）考核要求

1.了解线性空间的定义和性质；

2.理解并熟练掌握线性空间的基与维数，基的过渡矩阵的概念及求法，了解其性质；

3.理解子空间的定义和判定条件，掌握子空间的运算，维数公式；

4.掌握线性空间的和与直和；

5.理解线性空间的同构；

第七部分  线性变换

（一）考核知识点

1.线性变换的概念, 值域与核（理解）；

2.线性变换的运算（理解）；

3.线性变换与矩阵关系（掌握）；

4.特征值与特征向量（熟练掌握）；

5.矩阵对角化及判定（理解）；

6.不变子空间及空间的分解（了解）；

（二）考核要求

1.理解线性变换的概念, 值域与核；

2.理解线性变换的运算；

3.掌握线性变换与矩阵关系；

4.熟练掌握特征值和特征向量的概念及计算；

5.理解矩阵对角化及判定；

6.了解不变子空间及空间的分解；

第九章  欧几里得空间

（一）考核知识点

1.欧氏空间的定义与性质，度量矩阵（了解）；

2.正交基，标准正交基（理解并熟练掌握）；

3.Schimidt正交化（掌握）；

3.欧氏空间的同构（了解）；

4.正交变换的定义及判定条件（理解）；

5.欧氏子空间及正交补（理解）；

6.实对称矩阵的相似标准形，对称变换（掌握）；

（二）考核要求

1.了解欧氏空间的定义与性质，理解并熟练掌握度量矩阵的概念及求法；

2.理解并熟练掌握正交基与标准正交基；

3.掌握Schimidt正交化过程；

4.了解欧氏空间的同构；

5.理解正交变换的定义及判定条件；

6.了解欧氏子空间及正交补；

7.掌握实对称矩阵的相似标准形，对称变换；

 

Ⅲ.考试形式及试卷结构

一、考试形式

闭卷、笔试，试卷满分为100分，考试时间为120分钟，考生使用答题卡和试卷两部分答题．

二、试卷内容比例

多项式、行列式、线性方程组和矩阵             约占60%

二次型、线性空间、线性变换和欧几里得空间     约占40%

三、试卷结构与试卷题型比例

试卷有四种题型：单项选择、填空题、计算题和证明题．

单项选择题                约占20%

填空题                    约占20%

计算题                    约占30%

证明题                    约占30%

四、试卷难易度比例

试题按其难度分为容易、中等题、难题，三种试题分值的比例为4：4：2.