高等代数中的数学建模实例示范
案例1(货物交换的经济模型--知识点:线性方程组)
货物交换的经济模型:诺贝尔经济学奖获得者列昂杰夫(Leontief)考虑的一个经济学模型。 在一个原始部落, 根据分工, 人们分别从事 3 种劳动:农田耕作(记为 F)、农具与工具的制作(记为 M), 以及织物的编织(记为 C), 人们之间的贸易是实物交易。图 1 给出这 3 组人之间的交易系统, 图中所示表明, 农夫们将每年收获的一半留给自己, 并分别拿出1/ 4 给工匠们和织布者们;而工匠们却平均分配他们制作的用具给每个组;织布者们则留下 1/ 4 的衣物给自己, 并拿出 1/ 4 给工匠们、1/ 2 给农夫们。 此交易系统也可以用表给出, 见表 1。
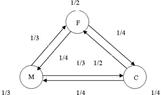
图 1 3 组人之间的交易系统
表 1 交易情况表

随着社会的发展, 实物交易形式变得十分不方便, 于是部落决定用货币进行交易。 假设没有资本和负债, 那么如何给每类产品定价, 使其公正地体现旧有的实物交易系统呢?
令x1 为农作物的价值, x2 为农具及工具的价值, x3 为织物的价值, 那么由表 1 的第一行, 农夫们生产的价值应等于他们交换到的产品包括留给自己价值即有 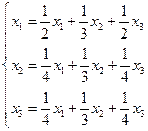
因此,该问题可归结为一个三元一次线性方程组的求解问题。 以此问题引出行列式, 使学生了解行列式与线性方程组的密切联系。 从简单的经济问题入手, 让学生了解知识的应用背景, 表明学习行列式是为生产实践服务的, 从而提高学生学习的积极性。
案例2(通信加密--矩阵的乘积与矩阵的逆)
加密技术在通信中有着重要的作用,加密 的 原 理 如 下:发送方采用某种算法,也就是密钥,将明文数据加密转化成密文数据后发送给接受方,接收方则可以采用对应的某种算法将密文数据解密转换成明文数据。从矩阵的角度来解释就是,明文用矩阵 X 来表示,加密密钥为矩阵 A ,则加密过程就是矩阵方程 AX =C ,密文是矩阵C ,解密密钥为矩阵B ,解密的过程为 X =BC ,加密技术是否有效,关键在于能否还原成明文。
我们来分析一下这两个矩阵方程,看这两个密钥矩阵 A,B 之间的关系。由于 AX =C,X =BC ,则有ABC =C ,即AB =E ,所以在保密通信中,密钥只有一个,解密密钥是通过这个关系式 AB =E 得 到 的,也就是加密密钥和解密密钥互为逆矩阵B = A-1 。比如,在2008年谍战 大 片《潜 伏》中,地下工作者余则成收到王翠平传递来的秘密消息,是20个 数 字,这 个 消 息 可 以用一个4行5列的矩阵来表示
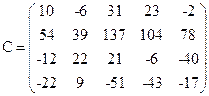
约定26个英文字母对应1到26个 数 字,0表 示 空 格,27表示 句 号。约定好的密钥是 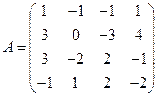
请问王翠平发来的密信是什么?
通过刚才的分析,现在想知道密信内容,就是要找到解密密钥,也就是约定好的密钥A 的逆矩阵,于是问题转换为逆矩阵的求解问题。计算|A|≠0,则方阵A 可逆,于是王翠平发来的信息就是

由英文字母与 整 数 间 的 对 应 可 得 到 密 信 内 容 为
“ACCOMPLISH THETASK。”
保密通信问题是当今信息时代发展的一个重要研究课题,实际的加密模型相当复杂,上面所举的例子只是为了说明逆矩阵应用的一个最简单的模型。
下一条:课外作业示范--共3个,协同完成
【关闭】